姚班校友揭“1.4×加速”陷阱：AI优化器为何名不符？

为了降低大模型预训练成本，最近两年，出现了很多新的优化器，声称能相比较AdamW，将预训练加速1.4×到2×。但斯坦福的一项研究，指出不仅新优化器的加速低于宣称值，而且会随模型规模的增大而减弱，该研究证实了严格基准评测的必要性。

一直以来，预训练，都是大模型训练过程中最花钱的部分。

比如，在DeepSeek V3中，它的成本占比就超过95%。

谁能在这里节省算力，就等于赚了。

长期以来，AdamW都是“默认选项”。但最近两年，出现了很多新的优化器。

它们大都声称能够相比AdamW，将预训练加速1.4×到2×，但却很少能真正落地。

斯坦福大学的研究人员，认为问题主要出现在两个方法学缺陷上：

一些基线的超参数调得不当；

许多实验局限于较小辨模的设置，导致这些优化器在更广泛、更真实场景下的表现仍待验证。

论文地址：https://arxiv.org/abs/2509.02046

有趣的是，这篇论文的标题“神奇优化器在哪里”（Fantastic Pretraining Optimizers and Where to Find Them），正是“捏它”自《神奇动物在哪里》（Fantastic Beasts and Where to Find Them）。

不得不说，论玩梗还是大佬们厉害！

不同缩放范式下的加速差异

研究人员对比了大模型在不同缩放范式下的加速差异。

他们在四种不同的数据-模型比（相当于Chinchilla最优范式的 1×、2×、4×、8×）下进行基准测试，并将模型规模扩展到1.2B参数。

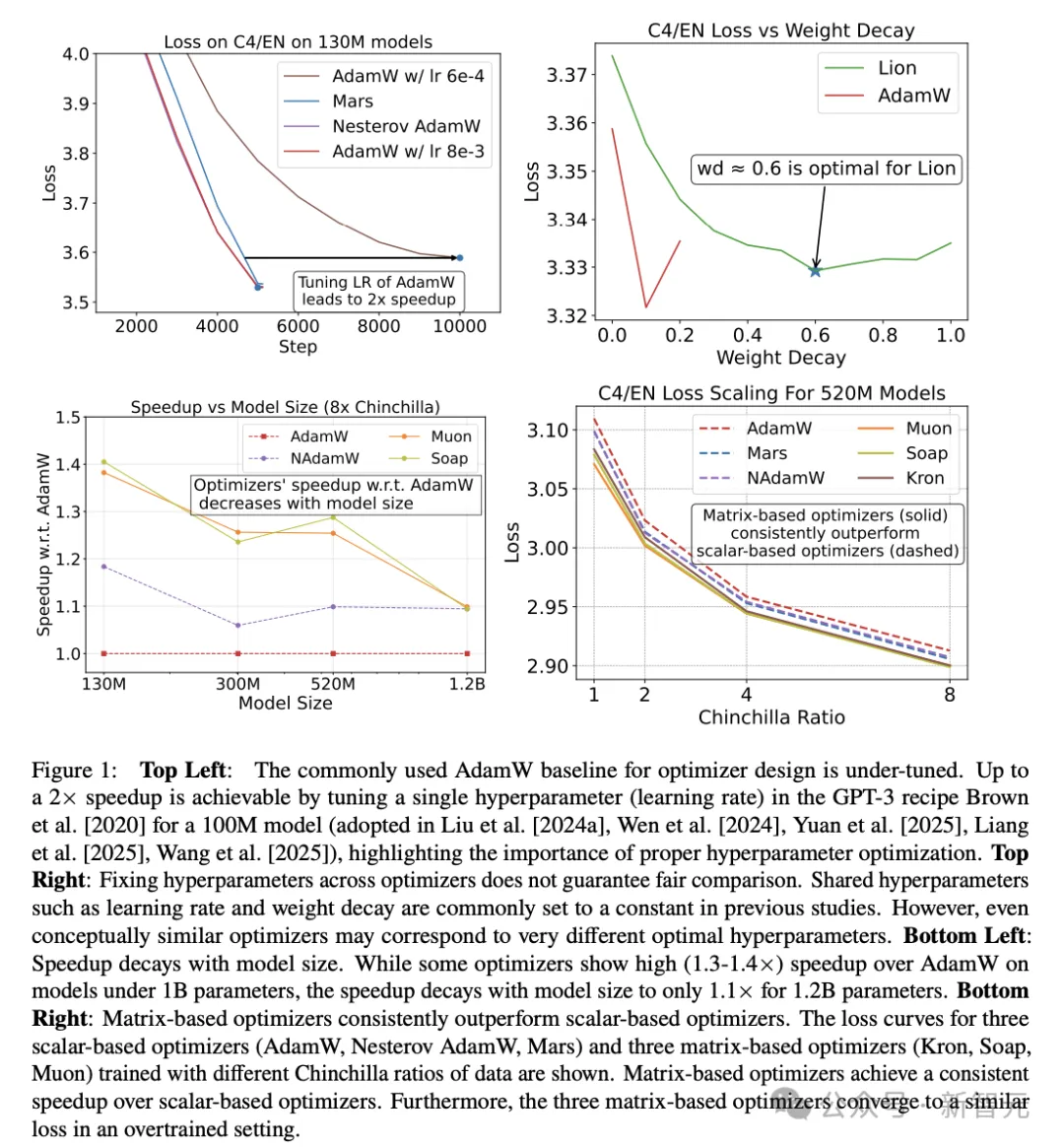
图1左上显示，在被广泛采用的GPT-3配方中，仅调一个超参数，就能让预训练获得2×的加速，这突显了正确超参数优化的重要性。

研究表明，在一系列模型规模和数据-模型比上，进行细致的超参数调优与训练结束时的评测是必要的，主要有三个原因：

首先，超参数不能盲目迁移，在优化器间固定超参数会导致不公平的比较。

第二，新优化器的加速低于宣称值，且随模型规模增大而减弱。相对于研究人员调优的AdamW基线，其他优化器的加速不超过1.4×。

此外，虽然Muon、Soap等新优化器在小模型（0.1B）上显示出1.3×加速，但在8×Chinchilla比例下的1.2B参数模型上，加速会降到约1.1×。

第三，早期的损失曲线可能产生显着误导。

在学习率衰减期间，不同优化器的损失曲线可能多次交叉，因此用中间检查点来评判优化器，得到的排名可能与在目标训练预算下比较的结果不同。

优化器设计的新见解

研究人员基于基准测试，带来了三个关于优化器设计的新见解：

1. 小模型更适合基于矩阵的优化器

研究人员发现，对于小模型，基于矩阵的优化器，持续优于基于标量的优化器。

基于标量的优化器（如AdamW、Lion、Mars等），需要通过标量操作逐个更新参数。

经过适当调参后，所有基于标量的优化器的优化速度与AdamW相近，平均加速比不足1.2×。

尽管其更新规则多样，但在小于520M参数的模型上，基于矩阵的优化器相对AdamW均可带来约1.3×的加速。

2. 最优优化器的选择，关键指标是“数据-模型比”

在1×Chinchilla范式下的赢家，随着数据-模型比提升，可能不再最优。

比如，在较小的Chinchilla比例下，Muon一直是表现最好的优化器。

但当数据-模型比增至8×或更高时，Kron和Soap的表现优于Muon（图3与图4）。

在本项研究中，研究人员研究了表1所列的11种优化器。

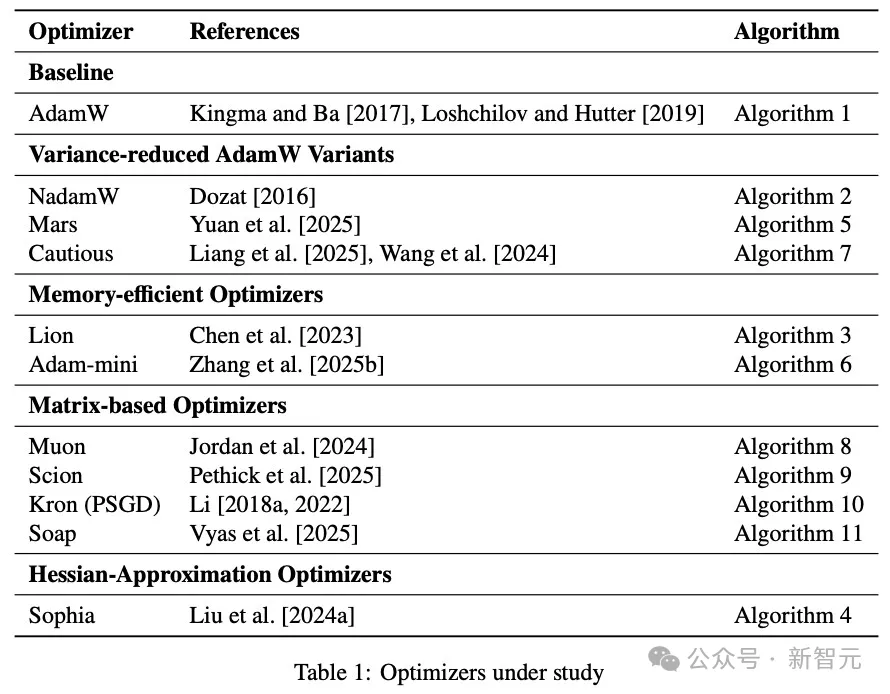
模型参数量，涵盖了130M、300M、520M、1.2B四种规模，详细超参数见表2。

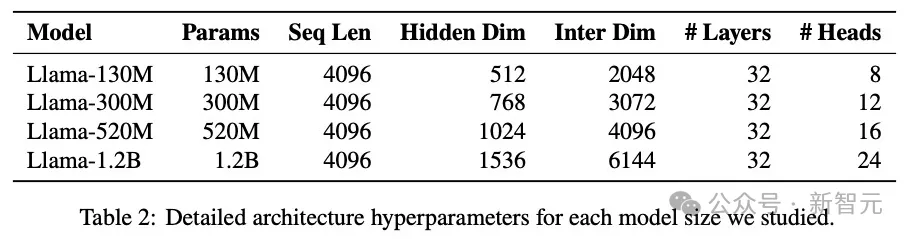
超参数的三种调参方式

按照不同阶段，研究人员对超参数采用了三种不同程度的调参方式：

阶段1：对超参数进行“细颗粒度”调参

研究人员在6种不同设置上执行该遍历，具体为1×Chinchilla下的130M、300M、500M，以及2×、4×、8×Chinchilla下的130M。

对于每个优化器以及上述六种范式，研究人员都找到了一个按坐标的局部最优解。

表3是一个针对300M参数、1×Chinchilla的AdamW示例性超参数优化过程。

阶段2：着重调整对“尺度敏感”的超参数

由于广泛调参在更大规模实验上代价过高，所以，研究人员对该过程进行了简化，着重调整对“尺度敏感”的超参数。

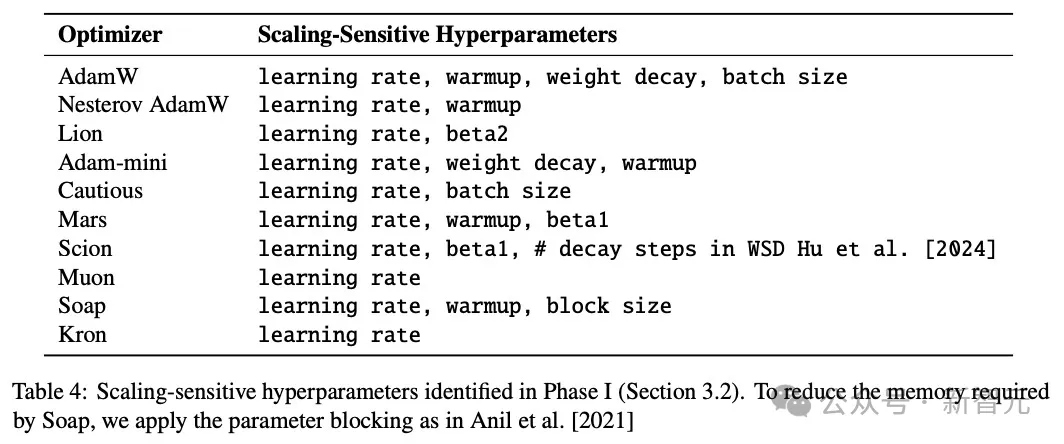
如表4，研究人员仅将对尺度敏感的超参数带入阶段2，从而把下一轮调参对象集中在那些跨尺度确实需要重新调参的超参数上。

通过这组实验，研究人员观察到两点现象：

1.基于矩阵的优化器始终优于基于标量的优化器，但所有优化器相对AdamW的加速比都不超过1.5×；

2.在基于矩阵的优化器内部，Muon在1–4×Chinchilla比例下表现最佳，但随着Chinchilla比例提高，会被Soap与Kron反超。

阶段3：为进一步外推而建立超参数缩放律

研究人员基于阶段2获得的优化超参数设置，拟合一个平滑的缩放律，用以预测每个随尺度敏感的超参数的最优值。

作为模型大小N，与数据预算D的函数，研究人员将每个随尺度敏感超参数h的最优值建模为：

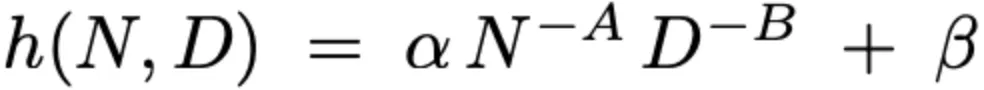
其中A、B、α与β为学习得到的系数。

研究人员在每个优化器的12个观测三元组(N，D，h)上，用非线性最小二乘来估计这些参数，使预测与真实最优超参数值的平方误差最小。

为检验预测质量，研究人员在N=1.2B、Chinchilla=1的设置下对AdamW运行了完整的阶段1遍历，并将识别出的最优解与拟合出的超参数进行对比。

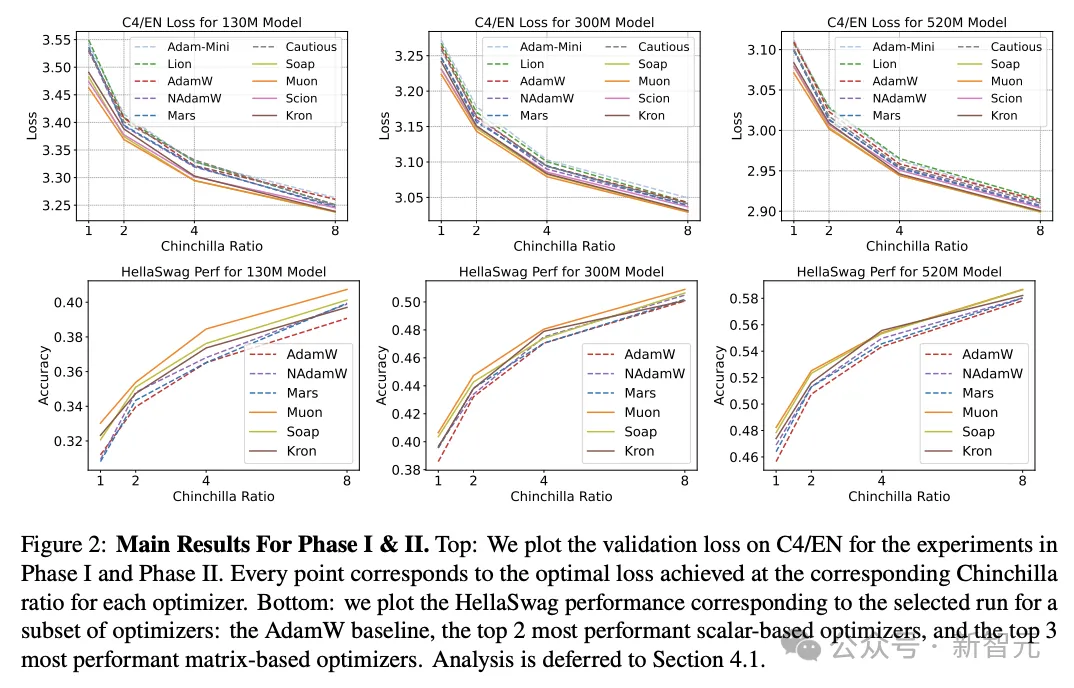
在图2上图中，研究人员绘制了两个阶段的C4/EN验证损失；在图2下图中，研究人员绘制了为部分优化器选择的运行所对应的HellaSwag表现。

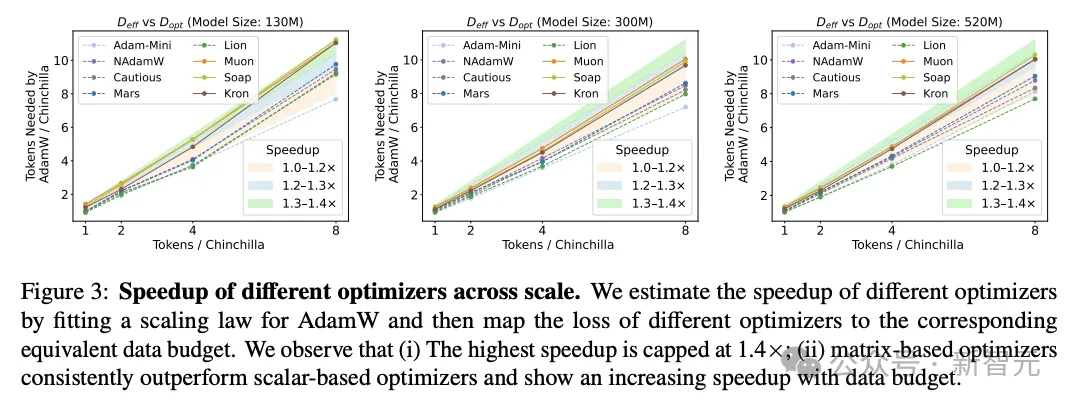
在图3中，显示了跨尺度的不同优化器加速。

研究人员通过为AdamW拟合缩放律，并将不同优化器的损失映射到对应的等效数据预算来估计加速，得到了以下二点观察：

1. 最高加速被限制在1.4×；

2. 基于矩阵的优化器始终优于基于标量的优化器，且随数据预算增加呈现更高的加速（表现出超线性趋势）。

实证发现

1. 在0.1B–0.5B参数模型上的结果

在所有模型规模与算力预算下，方差减少类的Adam变体（NAdamW、Mars、Cautious）与基于矩阵的优化器都相对AdamW基线，带来了加速。

然而，没有任何方法达到了过往文献声称的2×的加速。

研究人员得出如下结论：

（1）基于矩阵的方法优于基于标量的方法。加速比随数据预算增加而上升，但随模型规模增大而下降。

（2）方差削减技术带来小而稳定的提升。

在基于标量的家族中，所有方差削减型的Adam变体（NAdamW、Mars、Cautious）都稳定地超过vanilla的AdamW——仅在最小辨模实验上有轻微落后。

（3）AdamW的内存高效变体与AdamW的表现保持紧密。

两种内存高效的AdamW变体（Lion、Adam-mini），尽管辅助状态更少，其表现与AdamW紧密跟随，最多仅慢5%，有时甚至优于AdamW。

2. 在1.2B参数模型上的结果

研究人员利用拟合的超参数缩放律，将模型规模扩大到1.2B，以考察优化器的加速如何随模型规模变化。

观察到NAdamW、Muon与Soap依然相对AdamW带来加速，但这些优化器的加速减弱到约1.1×（图4，左与中），且不再带来下游改进（表 5）。

3. 高数据-模型比

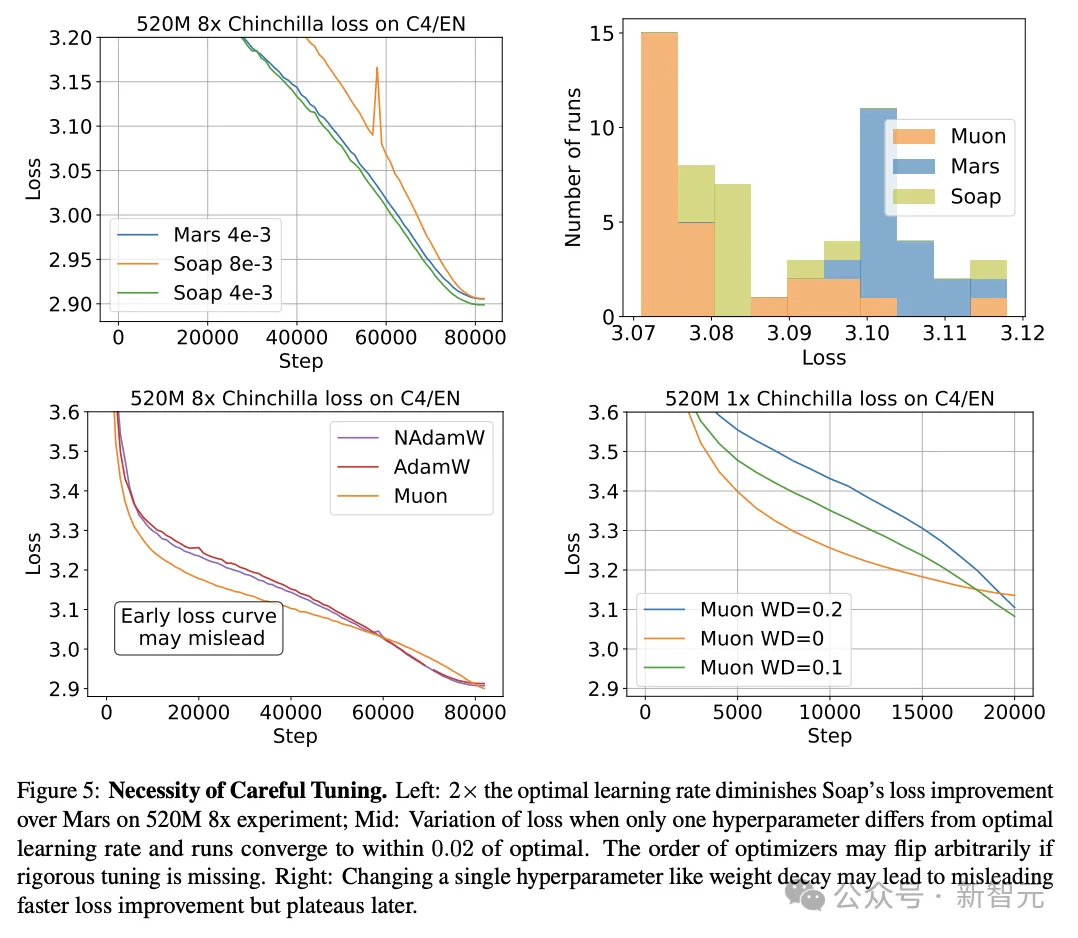
在130M与520M模型的8×Chinchilla范式下，Muon已被Soap超过。

为进一步验证，研究人员将三份300M模型训练到16×Chinchilla，并确认当数据-模型比增加时，Muon不再是最优优化器（图4，右）。

研究人员推测，当数据-模型比增大时，Soap与Kron保持的二阶动量会更有效。从长期看，对参数方向异质性的自适应可能带来更大的加速。

该研究证实了严格基准评测的必要性。

各优化器的共性现象

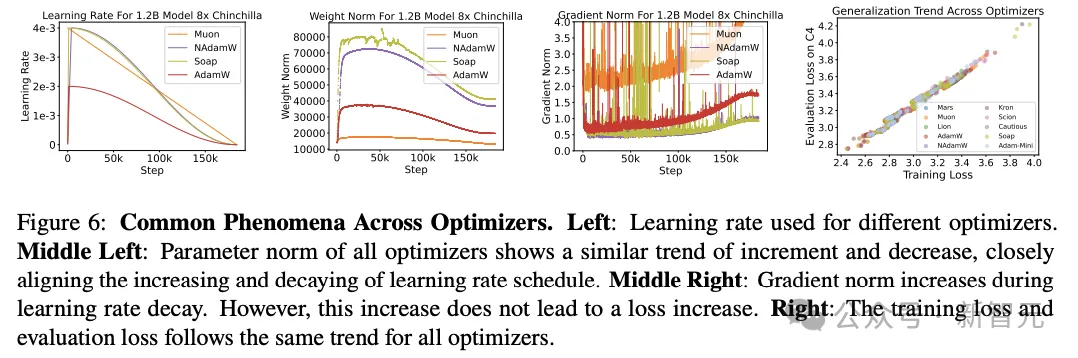
研究人员在预训练中，通过对11种深度学习优化器进行了基准评测，发现它们相对AdamW的真实增益远小于此前报道。

由此，研究人员强调了三个关键教训：

1.许多声称的加速源于超参数调优不足，因为公平的扫参会消除大多数表面的优势；

2.基于早期或不一致的评估进行比较可能具有误导性，因为在完整训练轨迹上优化器的排名常会发生变化；

3.即使表现最好的替代方桉也只提供温和的加速，且随模型规模增大而进一步减弱，在12亿参数时降至1.1×。

作者介绍

Kaiyue Wen

Kaiyue Wen是斯坦福大学的博士生。目前在马腾宇 (Tengyu Ma) 的课题组进行轮转，同时与Percy Liang老师合作。

他本科毕业于清华大学姚班，期间获得了获得了马腾宇、刘知远、Andrej Risteski、张景昭、王禹皓以及李志远等多位老师的指导。

他的研究兴趣涵盖深度学习的理论与应用，长远目标是理解深度学习背后的物理学原理，并坚信理论分析与实证研究相结合是实现这一目标的关键。

马腾宇（Tengyu Ma）

Tengyu Ma是斯坦福大学计算机科学系和统计系的助理教授。

他本科毕业于清华姚班，于普林斯顿大学获得博士学位。

他的研究兴趣涵盖机器学习、算法理论等方向，具体包括：深度学习、（深度）强化学习、预训练/基础模型、鲁棒性、非凸优化、分布式优化以及高维统计学。

Percy Liang

Percy Liang是斯坦福大学计算机科学副教授，兼任基础模型研究中心（CRFM）主任。同时也是CodaLab Worksheets的创建者，并借此坚定倡导科研工作的可复现性。

他专注于通过开源和严格的基准测试，提升基础模型（特别是大语言模型）的可及性与可理解性。

他曾围绕机器学习和自然语言处理领域进行了广泛研究，具体方向包括鲁棒性、可解释性、人机交互、学习理论、知识落地、语义学以及推理等。

此前，他于2004年在MIT获得学士学位，并于2011年在UC伯克利获得博士学位。