苏州大学首篇数学四大刊

中国学者又一篇数学四大刊成果出炉，还是苏州大学的首篇四大刊成果。

论文《Khintchine dichotomy for self-similar measures》已被Journal of the American Mathematical Society（《美国数学杂志》）录用。

该项成果的作者是苏州大学副教授张涵，合作者有Timothée Bénard （法国国家科学研究中心 (CNRS)，巴黎北索邦大学 (LAGA) 的研究员）和何伟鲲 （中国科学院数学与系统科学研究院副研究员）。

《数学年刊》《数学学报》《数学新进展》和《美国数学杂志》并称为数学四大刊，是国际数学界公认的数学顶级期刊，每年中国研究机构中选论文经常不超过10篇。

这次的突破是把描述有理数如何近似表达实数的辛钦定理推广到了所有自相似测度上。

接下来咱就看看是怎么个拓展法。

从勒贝格测度到所有自相似测度

要理解这项研究的价值，首先得先说说两个关键概念——辛钦定理和自相似测度。

辛钦定理是概率论中大数定律的一个核心结论，从理论上揭示了独立同分布随机变量序列的算术平均值，会依概率收敛到其共同的数学期望。

也就是解释了我们日常生活中一个默认的现象：当样本足够多时，样本的平均值会靠近总体的真实平均值。

在数论分支上，它还有一个重要的应用，就是用来描述有理数逼近实数的规律。

像π这样的实数，没办法用一个有理数精确表示，但总能找到一个分数，让它和这个实数的差距缩小到我们想要的任意精度。

比如用22/7逼近π，误差不到0.0015；用355/113逼近π，误差更是能缩小到千万分之三。

而数论领域的辛钦定理，就从数学层面量化了这种逼近的可能性和效率。它给出了一个明确的判定规则，告诉我们什么样的实数，能被有理数以多快的速度逼近，以及这种高效逼近的有理数，到底是稀有还是常见。

而这个判定规则，关键看一个特定的逼近函数ψ的求和是否发散——发散则好逼近的点多，收敛则好逼近的点少。

不过，之前辛钦定理多适用于勒贝格测度，也就是长度、面积、体积等常规度量。

而这次论文将其推广到自相似测度，关键性质是局部与整体的分布规律相似。

与均匀的勒贝格测度不同，它会根据自相似集合的结构，把测度质量集中在集合的关键部分。

如果把一个带有自相似测度的集合放大或缩小一定比例，得到的局部集合的测度分布，和原来的整体集合的测度分布是成比例复刻的。

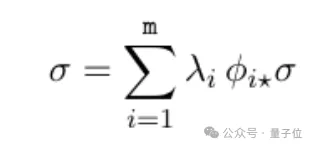
这类测度广泛存在于分形几何、动力系统等领域。最典型的例子就是中间三分之一康托尔集（通过无限次三等分线段、去掉中间一段形成的分形）上的测度。

此次研究通过三个关键理论支撑实现了突破。

一是定理A直接确立了自相似测度下的辛钦二分法，与经典定理形式保持一致；

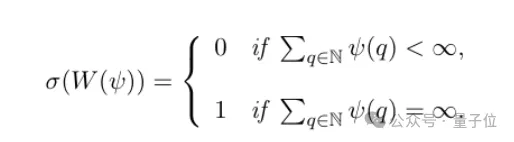
二是定理B证明了自相似测度在扩展变换下的有效等分布，并给出了误差估计。

听着玄，其实就是随着变换推进，测度会越来越均匀地铺在空间里，而且能算出不均匀的程度有多小，也就是能精准知道什么时候能近似均匀分布。

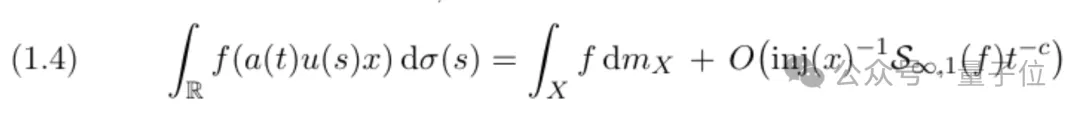
三是定理C通过研究特定随机游走的等分布特性，为前两项定理提供了坚实基础。

随机游走可以理解成：每次按概率选一个方向走一步，多次后形成的轨迹分布。

定理C证明这种随机游走的轨迹分布，也能实现有效等分布。

而定理A要的“自相似测度规律”、定理B要的“扩展变换下的均匀分布”，本质上都和“测度如何随变换/步数均匀化”有关。

定理C先把“随机游走的均匀化规律”搞清楚了，后面定理A和B只需要把自相似测度放进这个框架里，就能顺理成章地推出结论。

这一系列证明也彻底解决了1984年数学家Mahler提出的康托尔三分集上的丢番图逼近问题。

这个问题的核心就是想知道分形上的无理数能否被有理数有效逼近，以及逼近规律是否与普通线段一致。

如今，论文给出了明确答案：分形与普通线段的逼近规律完全相同，依然由ψ函数的求和敛散性决定。

这项成果打通了齐次动力系统、分形几何、数论三大领域的研究路径，为后续交叉学科研究提供了重要借鉴。

作者介绍

Timothée Bénard， 是法国国家科学研究中心（CNRS），巴黎北索邦大学 （LAGA） 的研究员。

研究兴趣在于李群及其离散子群商群上的随机游走，研究领域主要是概率论、动力系统、调和分析和李群理论。

何伟鲲，2017年博士毕业于巴黎第十一大学。

随后分别在耶路撒冷希伯来大学与韩国高等研究院任博士后。

2022年初入职中国科学院数学与系统科学研究院，任副研究员。研究兴趣包含齐次动力系统、分形几何、几何。

张涵，博士毕业于俄亥俄州立大学，后进入清华大学进行博士后研究。

2023年10月入职苏州大学，被聘为校优秀青年学者、特聘副教授，研究方向为齐性动力系统及其在数论中的应用。